算法通识与部分基础算法

  • 算法的定义：解题方案的准确而完整的表述，一系列解决问题的清晰表述
    （解决问题的方法，优劣取决于时间复杂度和空间复杂度，即运行时间和内存限制）
  • 时间复杂度：一种衡量算法运行时间长短的指标，是时间随输入规模增长而增长的量度（斜率）
    *空间复杂度即内存随输入规模增长的量度（斜率）
  • 大O表示法：算法的渐进时间复杂度
    函数或基本操作重复执行次数T(n)，设T(n)=time(1+2n)，当n足够大1可以忽略不计，倍数较小时，对于时间复杂度的影响不是很大，通常将常数简化，即T(2n)=O(n)，表示一个阶级的时间复杂度
  • 常数阶 O(1) 常量级别
  • 线性阶 O(n) 循环
  • 二次方阶O(n^2) 2层循环
  • 对数阶 O(logN) for(int i=1 ; i<=n ; i*2) 即自增呈指数型增长时为对数阶
    if( j % i ==0 ) 这种判断也是对数阶
  • 指数阶 O(2^n) for (int j = 1; j <= i * i; ++j) 即判断呈指数型增长时为指数阶
  • 总时间复杂度,例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
for (int i = 1; i <= n; ++i)
{
    for (int j = 1; j <= i * i; ++j)
    {
        for (int k = 1; k <= j; ++k)
        {
            ++sum;
        }
    }
}
//时间复杂度是 n * n^2 * n^2 = O(n^5)

for (int i = 1; i <= n; ++i)
{
    for (int j = 1; j <= i * i; ++j)
    {
        if (j % i == 0)
        {
            for (int k = 1; k <= j; ++k)
            {
                ++sum
            }
        }
    }
}
//时间复杂度是 n * n^2 * n^2^1/2 = O(n^4)

部分基础算法

  • 贪心：问题分为若干步骤，每次选取最优的选择，以保证总体最优（走一步看一步）

  • 这要求我们在每一步时使用尽可能少的嵌套递归等，以下是一个抽象的实例：
    1.最优情况肯定是增加数字总位数，每增加一位相当于原数字乘10
    2.而需要线段数量最少的就是’1’，所以能添‘1’就尽量添‘1’（2条线段）
    3.如果线段总条数为奇数会剩余一条线段，而’7’刚好需要三条线段，把第一位数字改为’7’即可
    4.这样我们就用最小的线段数组成了最大的数字

  • 前缀和(即S，前缀到前缀之和)：
    时间复杂度高达n*a*q，我们是否可以用其他方式减少时间复杂度呢

  • 举例：求第i项到第r项的和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//设i到r有n项，则时间复杂度为O(m*n)
while(m个询问，每个询问对应一对l和r){
    for(i=l;i<r;i++){
        sum+=a[i];  //每次询问都要重新算一遍
    }
    printf("%d",sum)
}
//而我们先使用前缀和做个预处理，定义sum[]数组，sum[i]代表a数组中前i个元素的和
while(m个询问){
    sum[0] = 0;  //初始条件
 for(i=l;i<r;i++){
     sum[i]=sum[i-1]+a[i]
 }
 printf("%d",sum[r]-sum[i-1])
}
//将时间复杂度由O(m*n)将为O(m+n)，相当于从O(n)将为O(1)，不用每次重复sum[n]之前的进程（简化）
  • 原数组变为二维数组怎么解决？：每次询问变为了(x1, y1) 到 (x2, y2)这一范围内数组的和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//首先,(1,4)-(4,1)~(1,1)-(4,4)，因此每次询问时把(x1,y1)改为较小的x和y，把(x2,y2)改为较大的x和y
//可以使用define宏定义（可定义为任何表达式，只会简单的替换不会计算，建议加括号防止结果有误）
#define min(x,y) ((x)<(y)?(x):(y))  //define可以定义为带参数的宏（能当函数用无需指定参数类型）
#define max(x,y) ((x)>(y)?(x):(y))  //max是define定义的宏，x和y是形参，参数名可以重复使用
//max/x/y都不用指定类型
int i1 = min(x1, x2) - 1; // 将坐标调整为从0开始
int j1 = min(y1, y2) - 1;
int i2 = max(x1, x2) - 1;
int j2 = max(y1, y2) - 1;
//循环体部分：sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + a[i][j]
for (int i = 0; i < 3; i++) {
 for (int j = 0; j < 3; j++) {
  sum[i][j] = a[i][j];     //分开写，更加简便（代码更简洁，值得学习）
  if (i > 0) sum[i][j] += sum[i - 1][j];
  if (j > 0) sum[i][j] += sum[i][j - 1];
  if (i > 0 && j > 0) sum[i][j] -= sum[i - 1][j - 1]; 
  }
}
//print输出（这里只是简编书写，实际上也要用if单独输出(0,0)(1,0)(0,1)三种情况
printf("%d",sum[i2][j2] - sum[i1-1][j2] - sum[i2][j1-1] + sum[i1-1][j1-1])

*sum[x1][y1] = sum[x2][y2] - sum[x1][y2] - sum[x2][y1] + sum\[x1][y1]*

  • 处理前缀和即两个小区间的和减去重叠区间，再加上a[i][j]:
  • 即***sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j]***（写在循环体内）

二分

  • 二分查找；二分答案；浮点二分 即另外一半不符合条件的舍去
  • 最简易的二分：
1
2
3
4
5
6
7
8
9
10
11
12
//这是求完数的一些代码
#include <stdio.h> 
int main() {
int N;
scanf("%d", &N);
for (int a = 1; a <= N; a++) {
 int c = 0;
 for (int b = 1; b <= a / 2; b++) if (a % b == 0) c += b;
 if (a == c) printf("%d ", a); 
return 0; 
}
//由于一个数的因子不可能大于本身的二分之一，因此用<=1/2限制范围减小运算量
  • 二分查找：*每次舍去一半区间，达到 log n的复杂度（要防止死循环）
1
2
3
4
5
6
7
8
int l=1 , r=n;
while(l<r){
 int mid=(l+r)/2;
 if(mid>num) r=mid;  //舍去右区间
 else l=mid+1;            //舍去左区间（奇数自动舍，所以+1，奇数实际上中间那个数左右都不要）
}
//比a+=1快很多,查找的次数呈对数级下降
//用右移（折半）符号也可以写二分查找

二分查找也称折半查找，就是每次查找去掉不符合条件的一半区间，直到找到答案
1.区间必须有单调性（不能来回跳，不然二分查找就无效了）
2.查找第一次出现的位置，如果查到一个值大于等于目标值，就把右半边放弃，因为右半边肯定也大于等于目标值；如果查到值比目标值小，那就放弃左半边
![[Pasted image 20231109201446.png]]
由长度 l+=1 直到算到最长的原木长度思路更改为 原木长度不断二分，直到二分小段数量等于需求数量
（大于还能更长，小于段数不够要缩短）

1
2
3
4
5
6
7
8
9
int l=1 , r=n;
while(l<r){
 int mid=(l+r)/2;
 if(mid小段数<需求数) r=mid;          //段数不够，需要缩短
 else if(mid小段数>需求数) l=mid+1;   //段数超过，还能加长
 else length=mid;                    //得到答案
}
//比a+=1快很多,查找的次数呈对数级下降
//用右移（折半）符号也可以写二分查找
  • 二分答案：
    1.答案在一个区间里
    2.能够判断答案是否正确
    3.具有单调性
  • 浮点二分
    1.同样是每次判断答案是否正确
    2.如果小于的话就将l赋为mid，即为舍弃左区间;如果大于就将r赋为mid，即为舍弃右区间
    3.最后当 r - l < 1E-n时，结束循环（ n可以自己设定，取决于精确度）

排序

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<stdio.h>
#define N 10 

int main(void)
{
 int arr[N] = { 0,3,2,5,8,4,7,6,9,1 };//创建一个大小为N的数组，方便理解算法
 int i = 0;//控制走访轮数
 int j = 0;//控制数组元素下标
 int temp = 0;//申请一个临时的空间（数组元素交换时需要一个临时空间）

 for (i = 0; i < N - 1; i++)//最多走访N-1轮
 {
  for (j = 0; j < N - 1- i; j++)//每一轮相邻元素只需比较N-1-i次即可
  {
   if (arr[j] < arr[j + 1])
   {
    temp = arr[j];
    arr[j] = arr[j + 1];
    arr[j + 1] = temp;
   }
  }
 }
 //for循环执行完毕，排序完成，依次打印出排序完成后的数组元素

 for (i = 0; i < N; i++)//变量i清零赋予新的意义：控制打印个数
 {
  printf("%d ", arr[i]);
 }

 return 0;
}

快速排序

1

快速排序的每一轮处理其实就是将这一轮的基准数归位，直到所有的数都归位为止，排序就结束了。

1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <stdio.h>
int a[101],n;//定义全局变量，这两个变量需要在子函数中使用
void quicksort(int left,int right)
{
    int i,j,t,temp;
    if(left>right)
       return;
    temp=a[left]; //temp中存的就是基准数
    i=left;
    j=right;
    while(i!=j)
    {
       //顺序很重要，要先从右边开始找
       while(a[j]>=temp && i<j)
            j--;
       //再找右边的
       while(a[i]<=temp && i<j)
            i++;
       //交换两个数在数组中的位置
       if(i<j)
       {
            t=a[i];
            a[i]=a[j];
            a[j]=t;
       }
    }
    //最终将基准数归位
    a[left]=a[i];
    a[i]=temp;

    quicksort(left,i-1);//继续处理左边的，这里是一个递归的过程
    quicksort(i+1,right);//继续处理右边的 ，这里是一个递归的过程
}
int main()
{
    int i,j,t;
    //读入数据
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);
    quicksort(1,n); //快速排序调用

    //输出排序后的结果
    for(i=1;i<=n;i++)
        printf("%d ",a[i]);
    getchar();
    getchar();
    return 0;
}

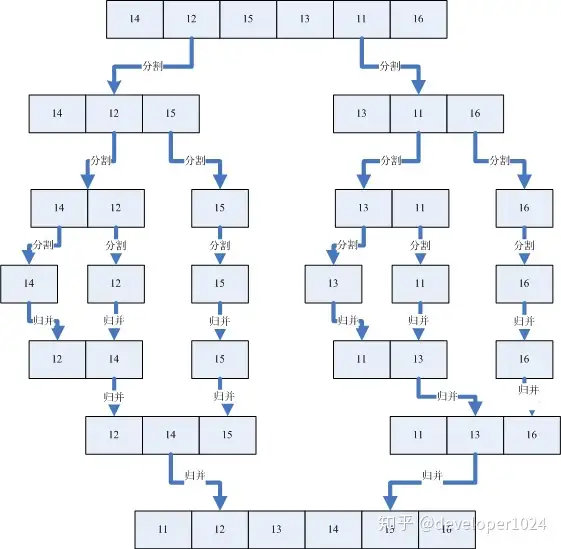
归并排序

1

具体的我们以一组无序数列｛14，12，15，13，11，16｝为例分解说明，如下图所示：

1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 归并排序（C-迭代版）
int min(int x, int y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int* a = arr;
    int* b = (int*) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int* temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 归并排序（C-递归版）
void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);

计数排序

1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 计数排序（C）
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
void print_arr(int *arr, int n) {
    int i;
    printf("%d", arr[0]);
    for (i = 1; i < n; i++)
        printf(" %d", arr[i]);
    printf("\n");
}
void counting_sort(int *ini_arr, int *sorted_arr, int n) {
    int *count_arr = (int *) malloc(sizeof(int) * 100);
    int i, j, k;
    for (k = 0; k < 100; k++)
        count_arr[k] = 0;
    for (i = 0; i < n; i++)
        count_arr[ini_arr[i]]++;
    for (k = 1; k < 100; k++)
        count_arr[k] += count_arr[k - 1];
    for (j = n; j > 0; j--)
        sorted_arr[--count_arr[ini_arr[j - 1]]] = ini_arr[j - 1];
    free(count_arr);
}
int main(int argc, char **argv) {
    int n = 10;
    int i;
    int *arr = (int *) malloc(sizeof(int) * n);
    int *sorted_arr = (int *) malloc(sizeof(int) * n);
    srand(time(0));
    for (i = 0; i < n; i++)
        arr[i] = rand() % 100;
    printf("ini_array: ");
    print_arr(arr, n);
    counting_sort(arr, sorted_arr, n);
    printf("sorted_array: ");
    print_arr(sorted_arr, n);
    free(arr);
    free(sorted_arr);
    return 0;
}